Assalamualaikum dan selamat berjumpa kembali.

Pada artikel yang lepas, saya telah memberi penerangan yang ringkas berkenaan kelemahan perceptron merujuk kepada masalah XOR dan bagaimana multilayer perceptron dapat menyelesaikannya. Saya juga ada melontarkan persoalan, "Mengapa algoritma yang berasaskan pada neural network ini terkubur selama hampir dua dekad ?", walaupun permasalahan XOR itu boleh diselesaikan oleh multilayer perceptron.

Permasalahan besar muncul apabila multilayer perceptron (MLP) itu ingin digunakan untuk di latih dengan data non-linearly separable yang sebenar, bukan setakat data yang sangat asas seperti masalah XOR itu. Mungkin anda terfikir, (ー_ーゞ

"Jika datanya kompleks seperti itu maka tambahkanlah dengan lebih banyak neuron dan lapisan hidden layer"

Bijak! memang tepat sekali jangkaan anda, tetapi sanggupkah anda menunggu proses training model itu selama beribu-ribu tahun? Tak berbaloi kan? Oleh kerana kegagalan para penyelidik ketika itu mencari kaedah melatih MLP dalam satu jangka masa yang munasabah lah yang menjadi punca utama mengapa neural network terkubur sekian lama.

Akhirnya pada tahun 1986, David Rumelhart, Geoffrey Hinton, and Ronald Williams telah memecah kebuntuan dengan memperkenalkan algoritma backpropagation yang berkait rapat dengan algoritma Gradient Decent (ini pernah di sebut di artikel pertama saya). Mungkin timbul beberapa persoalan di minda anda, ʕ ʘ̅͜ʘ̅ ʔ

"Kenapa namanya Backpropagation, takda nama lain ker? Apa kaitannya pulak dengan Gradient Decent? Benda yang sama jer kot nama sajer yang lain"

Di artikel yang sebelum ini saya ada menunjukkan pengiraan multilayer perceptron menyelesaikan masalah XOR bermula dari input layer, hidden layer, dan output layer kan? Ini adalah dinamakan neural network dengan proses feedforward sebab ia hanya melibatkan process yang maju kehadapan sahaja. Dengan adanya algoritma backpropagation, neural network ini berfungsi dengan dua arah iaitu ke depan dan ke belakang berulang kali.

"Melatih model dengan algoritma Gradient Decent (GD) menggunakan Backpropagation (BP) sebagai teknik pengkomputeran gradien ataupun kecerunan"

Frasa di atas mengambarkan hubungan antara kedua-dua algoritma tersebut iaitu GD adalah algoritma bagi mencapai kecerunan K=0 dalam masa T, manakala BP adalah algoritma yang penting untuk menjalankan proses pengiraan kecerunan tersebut dari setiap lapisan, dari depan hinggalah ke lapisan belakang neuron dengan efisien.

Kecerunan apa? mungkin ada yang tertanya-tanya. Ia adalah kecerunan ataupun slop yang terhasil oleh perubahan error terhadap perubahan parameter weight (k=de/dw). Dengan kata lain, berapakah nilai perubahan pada error jika nilai parameter weight berubah pada sesuatu nilai tertentu. Jika kecerunannya adalah 0 (zero) ataupun mendatar ia di anggap sebagai di mana nilai error e yang paling minimum telah di temui (pada satu titik nilai parameter weight w).

Secara analoginya, ia juga boleh di anggap seperti anda sedang mencuba turun dari atas bukit ke bawah kaki bukit dalam keadaan gelap. Anda terus menuruni cerun selagi anda merasakan kaki dan kepala menunduk ke bawah. Sebaliknya, anda akan berpatah ke belakang apabila anda merasakan kaki dan kepala anda mendongak ke atas. Anda terus-menerus mengulangi proses turun dan naik cerun itu sehinggalah anda yakin yang anda sudah berada di kawasan tanah rata. Proses GD ini boleh digambarkan seperti di bawah (Y adalah fungsi error atau cost manakala X adalah parameter weight).

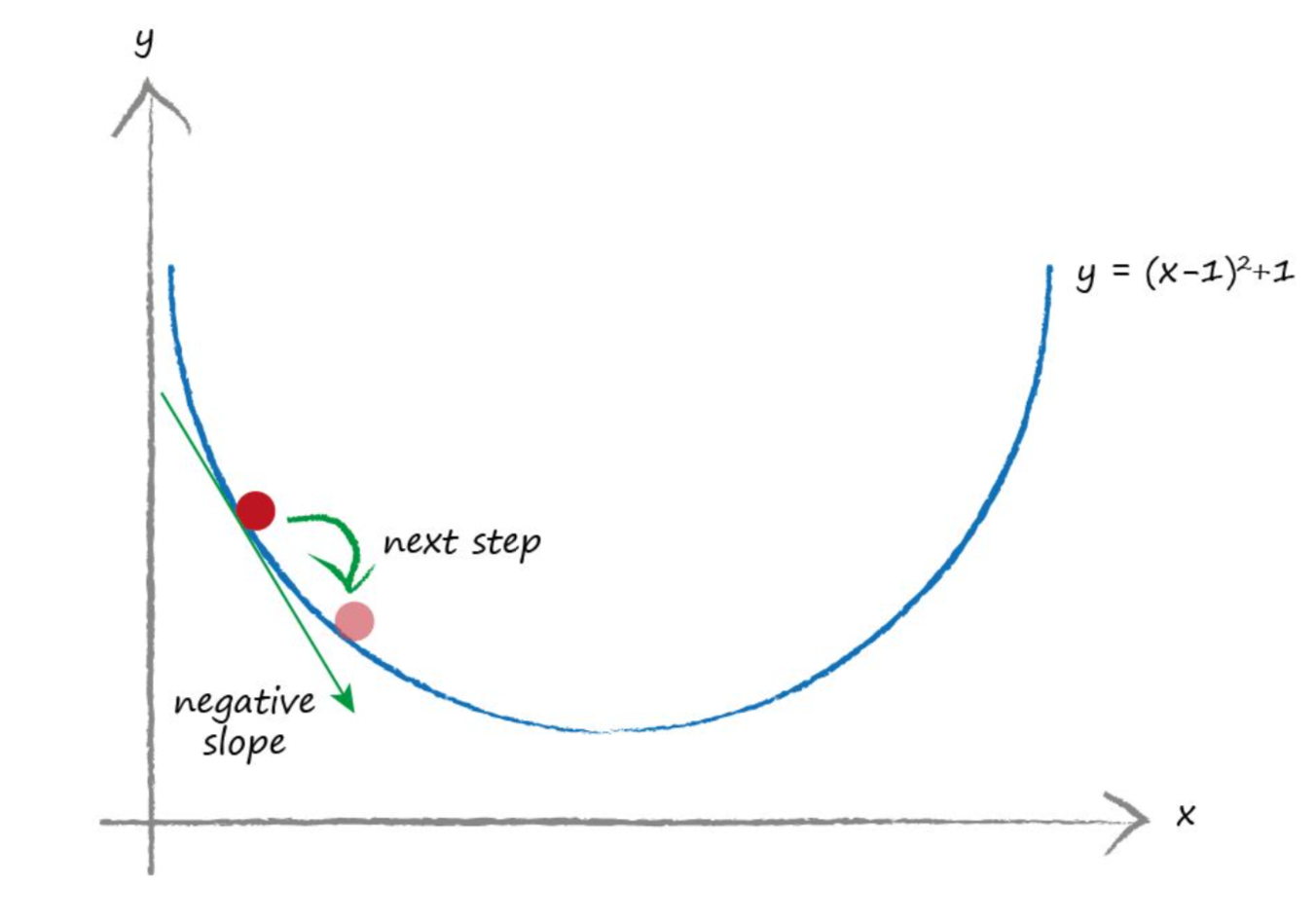
Anda masih ingat lagi pada artikel yang lepas, Pengenalan Kepada Perceptron?, saya ada menyatakan yang kita perlu "tune" kelajuan training model melalui learning rate. Supaya ia tidak terlalu laju dan tidak lah pula terlalu perlahan. Saya juga ada memberi analogi, "Seperti memasukkan benang ke dalam lubang di jarum" kan? Gambarajah di bawah memberikan gambaran yang lebih jelas mengapa kita perlu melakukan hyperparameter tuning pada learning rate setiap kali melakukan proses training model.

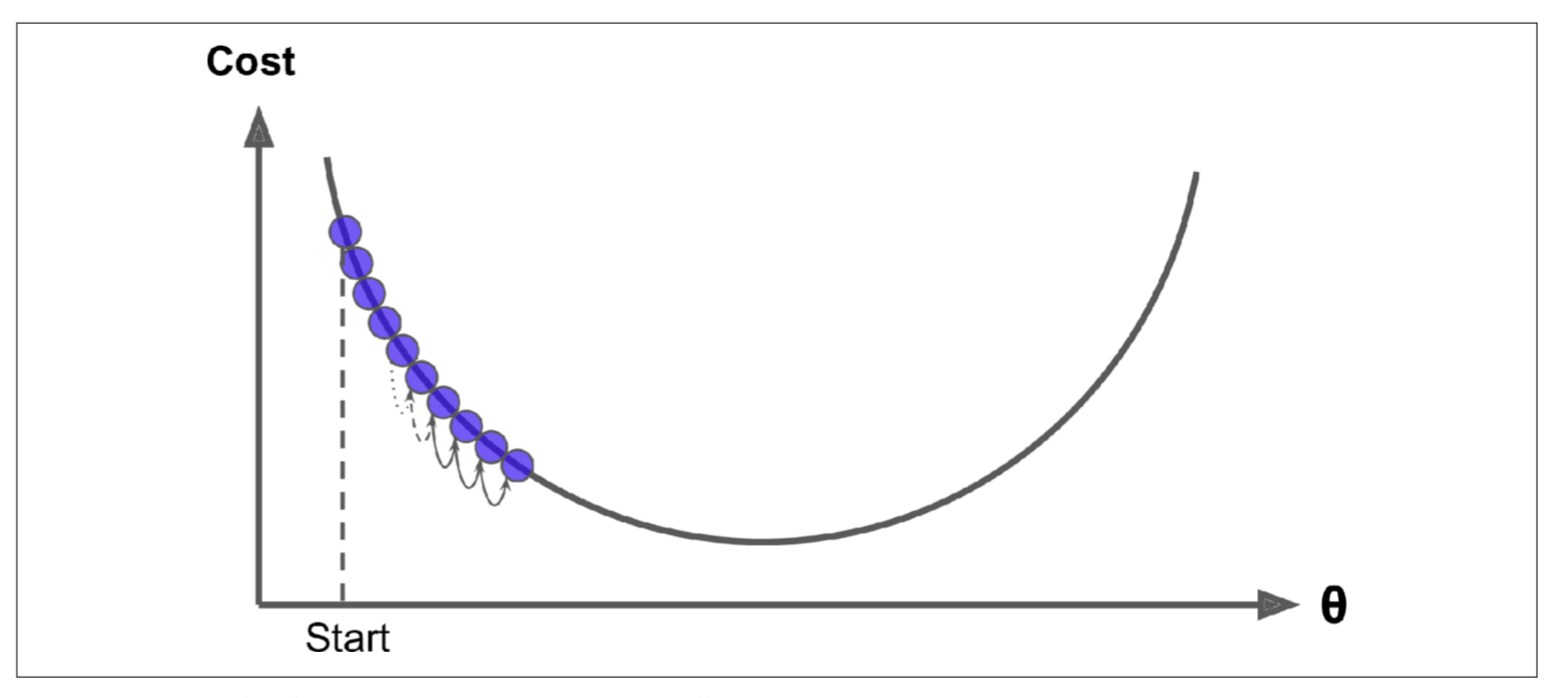
Gambarajah di atas menunjukkan nilai setting learning rate yang terlalu kecil. Walaupun ini memberi kebarangkalian yang lebih kepada algoritma GD untuk sampai ke titik paling rendah, tetapi ianya akan mengambil masa yang lama. Manakala gambarajah di bawah pula menunjukkan reaksi algoritma GD yang terpantul-pantul di sekitar cerunan tanpa berjaya sampai ke titik paling rendah apabila setting learning ratenya terlampau besar.

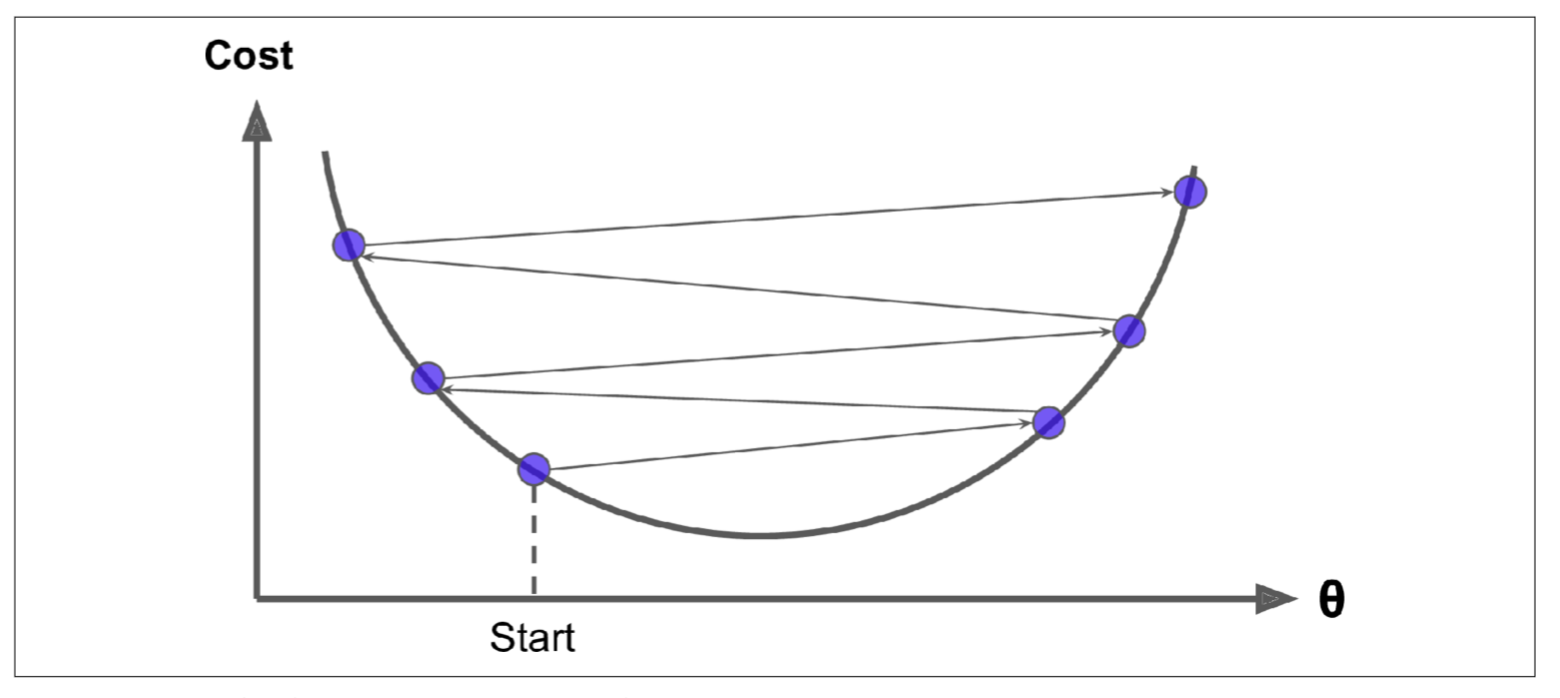
Namun, tidak semestinya bentuk cerun yang dihasilkan oleh fungsi error ataupun cost ini cantik bentuknya seperti di atas. Kemungkinan besar bentuk cerunannya adalah seperti gambarajah di bawah, terdapat lubang, lereng, dataran tinggi, dan segala macam permukaan yang tidak sekata, sehingga sukar untuk mencapai titik yang paling minimum.

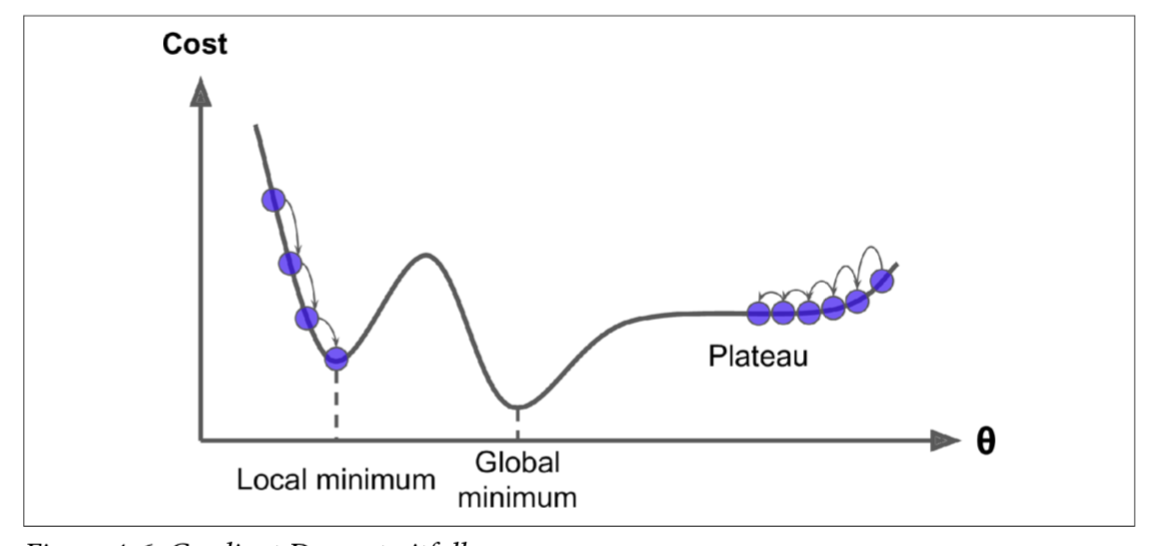
Seperti contoh, sekiranya algoritma GD bermula dengan nilai permulaan parameter weight di sebelah kiri (seperti di gambarajah), maka ia akan tersangkut di titik minimum yang di panggil local minimum, yang sebenarnya bukanlah titik paling minimum ( global minimum ialah titik minimum yang sepatutnya di capai ). Sebaliknya, jika nilai permulaan parameter weight bermula di sebelah kanan, ia akan memakan masa yang sangat lama untuk menyeberangi kawasan dataran tinggi. Jika anda berhenti iteration training terlalu awal, anda tidak akan sempat mencapai ke tahap global minimum itu. Untuk pengetahuan anda, ada banyak jenis algoritma optimization untuk algoritma GD ini yang boleh digunakan mengikut kesesuaian fungsi cost dan dataset, seperti RMSprop, Adam, AdaMax, AdaGrad, Momentum dan banyak lagi.

Berikut adalah penerangan yang lebih tersusun berkenaan proses feedforward dan backpropogation.

Proses ini berlaku pada setiap batch atau kumpulan kecil data. Misalnya, jika setiap batch adalah terdiri daripada 20 rekod data (1 batch = 20 rekod) dan jumlah kesemua rekod data adalah 1000 (1 epoch = 1000 rekod), maka proses ini berlaku sebanyak 1000/20 = 50 batch pada setiap epoch.
Feedforward bermula dari input layer, dan ke hidden layer pertama dan seterusnya. Feedforward mengira output di semua neuron pada setiap lapisan berdasarkan pada setiap batch data tersebut sehinggalah ke lapisan terakhir iaitu output layer, di mana nilai ramalan dihasilkan. Semua hasil pengiraan pada batch di setiap lapisan neuron tersebut disimpan kerana ia diperlukan untuk kegunaan proses backpropagation (1 batch = 1 iteration = 1 Feedforward + 1 Backpropogation).
Seterusnya, algoritma mengukur error di output layer (ia menggunakan fungsi error atau cost yang membandingkan output yang telah dilabelkan dan output ramalan) dan nilai error ini akan digunakan oleh backpropagation.
Kemudian ia menghitung berapa besarkah setiap sambungan weight output menyumbang kepada error tersebut (mengukur kecerunan k=de/dw). Ini dilakukan secara analitik dengan menggunakan "chain-rule" (salah satu ilmu asas matematik kalkulus dalam silibus SPM), yang menjadikan proses pengiraan ini cepat dan tepat.
Algoritma kemudian mengukur berapa banyak sumbangan error yang datang dari setiap sambungan weight di setiap lapisan neural network bergerak ke arah belakang sehinggalah ke lapisan input layer dengan menggunakan teknik chain-rule itu. Seperti yang dijelaskan sebelumnya, backpropagation ini mengukur kecerunan error terhadapan sambungan weight dengan efisen pada semua sambungan weight dalam setiap lapisan neural network dengan menyebarkan nilai kecerunan tersebut ke belakang.
Akhirnya, algoritma Gradient Descent beraksi dengan mengubah semua nilai weight di dalam setiap lapisan neural network berdasarkan pada nilai kecerunan atau gradien error yang dikira sebelum ini. Proses feedforward & backpropagation ini berlaku berulang-ulang kali berdasarkan pada jumlah epoch yang anda tetapkan.

Bagi membolehkan algoritma ini dapat berfungsi seperti yang diharapkan, fungsi activation step pada MLP itu perlu digantikan fungsi yang lain. Ini penting kerana fungsi step hanya mempunyai garisan menegak dan mendatar, jadi tidak ada kecerunan yang dihasilkan untuk kegunaan algoritma gradient descent. Oleh itu kita memerlukan fungsi activation yang "continuous & differentiable" iaitu fungsi yang boleh menghasilkan gradien atau kecerunan disepanjang garisan melalui perubahan error terhadap perubahan parameter weight. Ini membolehkan algoritma gradient descent bergerak menuju ke arah titik minimum pada setiap iteration. Berikut adalah beberapa fungsi activation yang biasa digunakan,

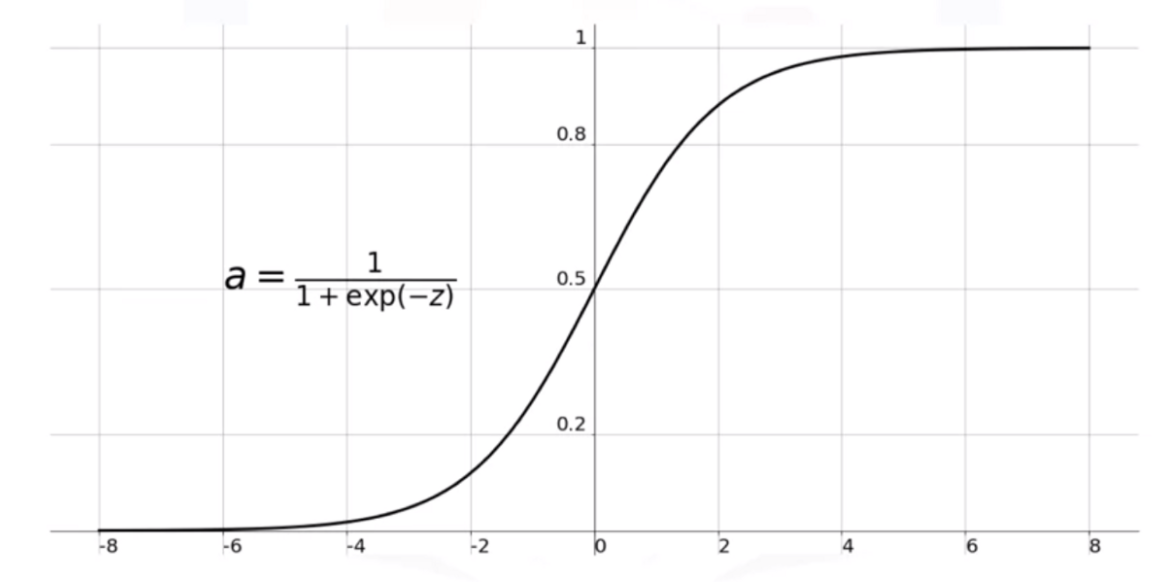
Fungsi sigmoid, σ (z) = 1 / (1 + exp (–z) ).

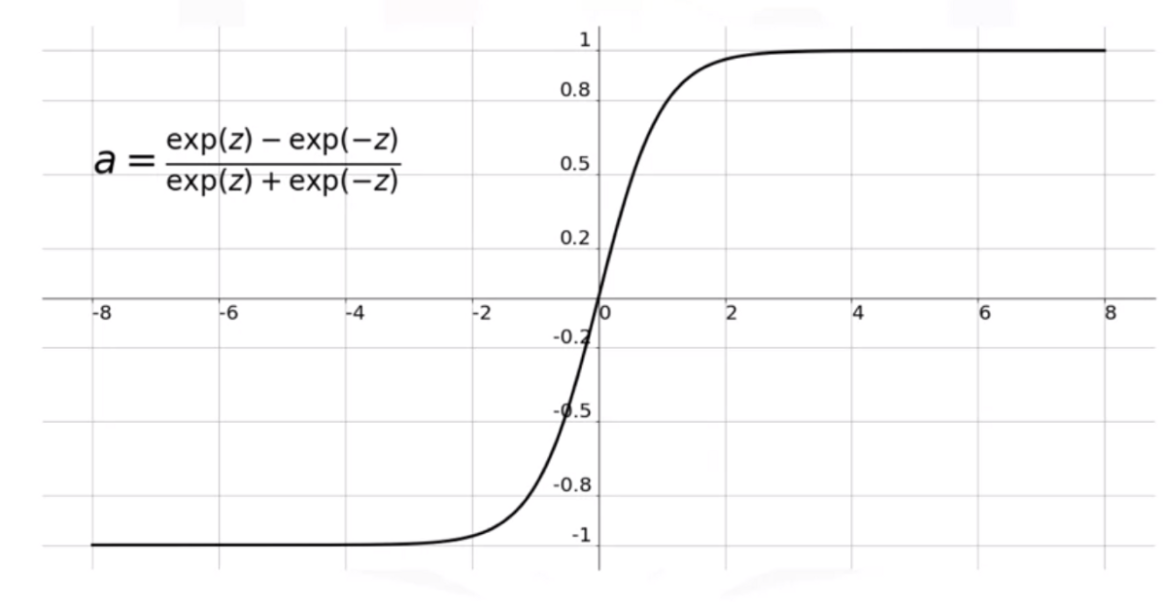
Fungsi tangen hiperbolik: tanh (z) = 2σ (2z) - 1

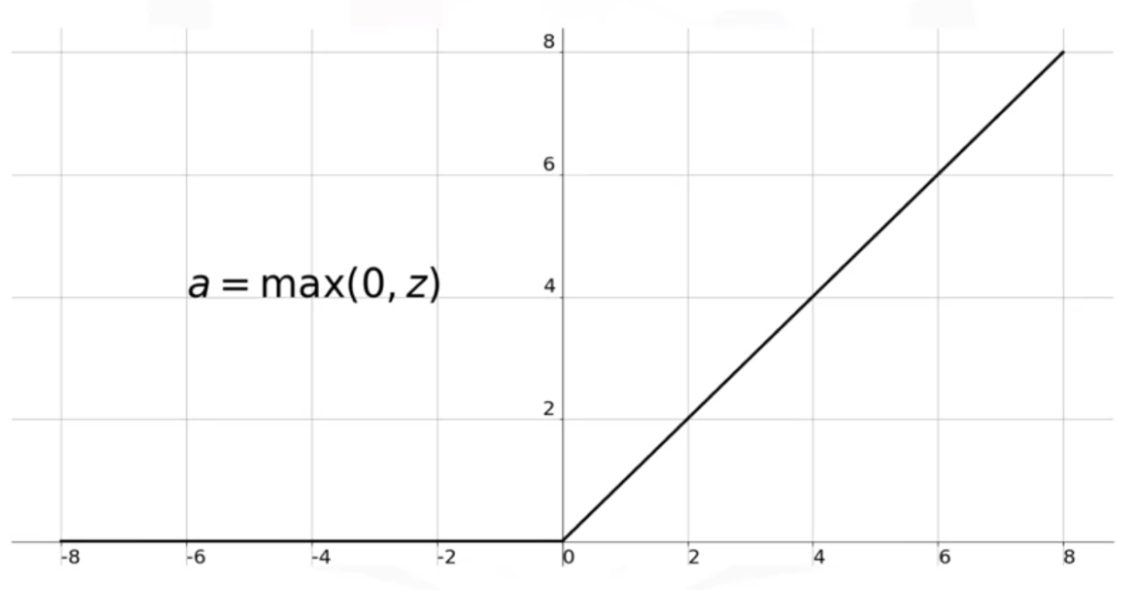
Fungsi Rectified Linear Unit, ReLU (z) = max (0, z)

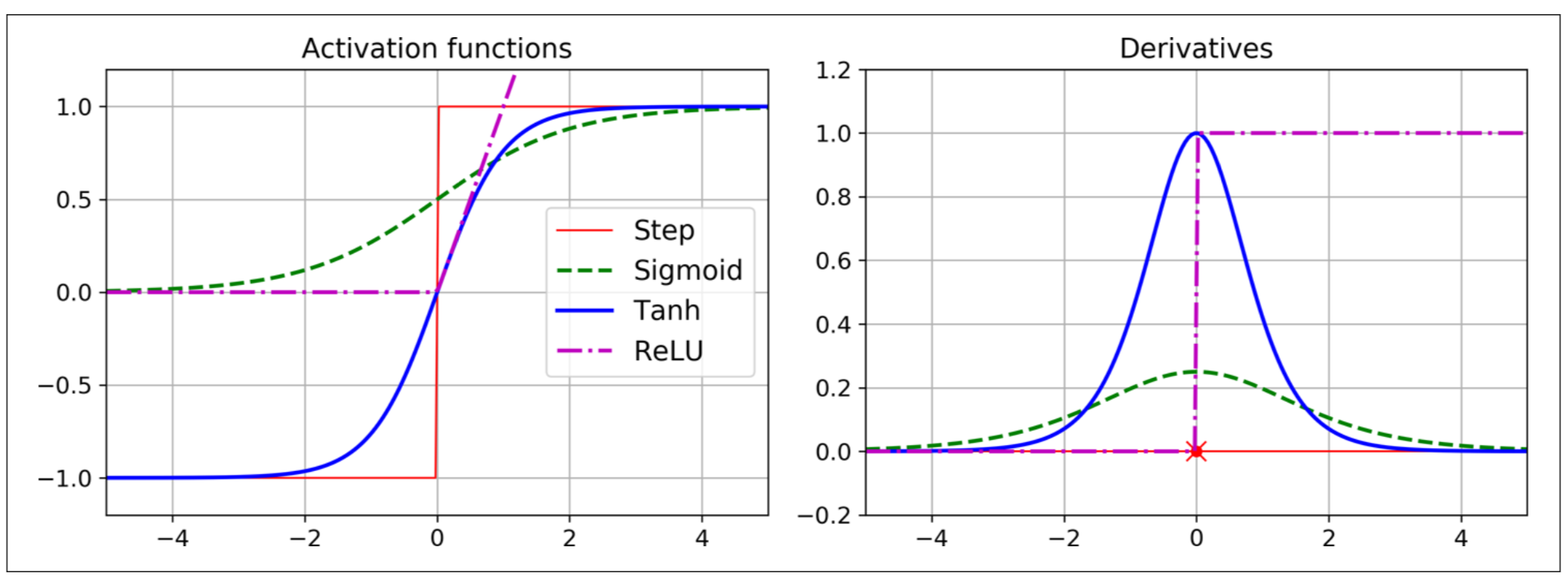
Gambarajah di bawah menunjukkan fungsi activation dan derivatifnya (di sebelah kanan). Kita akan bincangkan berkenaan fungsi-fungsi ini di artikel yang akan datang.

Oh ya, anda masih ingat satu lagi tujuan penting activation function yang pernah saya nyatakan sebelum ini? Ya! untuk membolehkan kita membina model non-linear bagi menyelesaikan permasalahan yang kompleks, kita menggunakan activation function seperti ini untuk menukarnya dari dunia linear ke dunia non-linear.

Kenapa? sebab jikalau ianya masih lagi dalam bentuk linear, maka takda maknanya pun kalau kita tambah hidden layer tu berlapis-lapis bagi tujuan untuk membina suatu model yang kompleks. Sebagai contoh, jika

f (x) = 2x + 3, dan g (x) = 5x - 1

Kemudian kita sambungkan kedua-dua fungsi linear itu (menjadi dua lapisan network), ia sebenarnya hanya menghasilkan satu lapisan fungsi linear sahaja.

f (g (x)) = 2 (5x - 1) + 3 = 10x + 1

Oleh itu, tak kiralah berapa ribu hidden layer pun yang anda tambah, akhirnya ia cuma menjadi satu fungsi linear yang berbeza nilai kecerunan dan ketinggiannya.

Ok lah, cukup di sini sahaja buat masa ini. Di artikel yang akan datang, insyaAllah saya akan tunjukkan satu contoh implementasi MLP Classification menggunakan Keras. ᕕ( ᐛ )ᕗ